はじめに
この記事では、第13章として「図形で習ういろいろな性質」について解説します。この章は、初級と中級の記事に分かれています。この中級の記事では、小学校で習った図形の性質として、「対称性」や「拡大図・縮図」などを順番に説明していきます。
初級では、「平行」「垂直」「合同な関係」などより基本的な英単語に触れています。興味のある方は下からどうぞ!
また今回の内容は、第11章と第12章の内容と関連しています。以下のリンクより一緒に読んでおくと、理解がより深まると思います。
→ 第11章:平面図形の特徴と種類(初級)
→ 第12章:立体図形の特徴と種類(初級)
(所要時間:10分)
単語・表現の一覧
| 単語・表現 | 意味 |
|---|---|
| symmetry | 対称 |
| line symmetry | 線対称 |
| point symmetry | 点対称 |
| axis of symmetry, line of symmetry | 対称の軸 |
| point of symmetry, center of symmetry | 対称の点 |
| enlarged diagram, enlarged figures | 拡大図 |
| reduced diagram, reduced figures | 縮小図 |
| scale factor | 尺度 |
| approximate figure, approximate shape | 概形 |
単語の解説
対称性についての英語表現
1.小学算数で習った対称性の確認
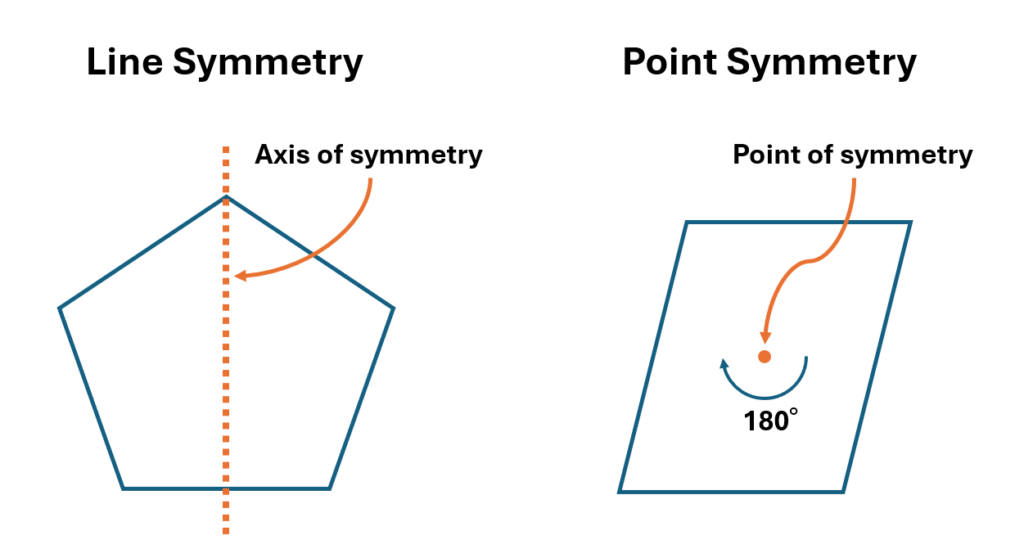
小学校で習う図形の対称性には「線対称」と「点対称」の2種類があります。
線対称:「対称の軸で図形を折り曲げたときにピッタリ重なる性質」
点対称:「対称の中心で図形を180°回転させたときにピッタリ重なる性質」
2.線対称・点対称を英語で言うと…
線対称は英語で「linesymmetry」、点対称は「point symmetry」と言います。
「symmetry」は数学で「対称」を表す単語です。
この対称性という性質は大学数学などでも学ぶような重要な数学の性質ですので、頑張って覚えましょう。
対称でない(非対称である)ことは「asymmetric」と言います。
先ほど紹介した「incongruence」や「disadvantage」、「irregular」など「~でない」を表す部分はいろいろあり難しいですね。
3.対称性に関連する英単語
線対称での「対称の軸」は「axis of symmetry」や「line of symmetry」と言います。
「axis」は軸という意味です。
点対称での「対称の点」は「point of symmetry」や「center of symmetry」などと言うことができます。
4.例文
英語で「対称である」と表現する方法には次のようなものがあります。
- The isosceles triangle has line symmetry.
(二等辺三角形は線対称である) - The isosceles triangle is symmetric about its axis of symmetry.
(二等辺三角形は対称の軸で対称である) - Find the symmetric figures.
(対称な図形を探しなさい) - Not all line-symmetric figures have point symmetry.
(すべての線対称な図形が点対称なわけではない)
*最初の2つの例文は同じことを意味しています
上の例文では「symmetric」という単語を使いましたが「symmetrical」に替えても文法的に意味は変わりません。
ただ、私の感覚では「symmetric」の方が数学では使われ、「symmetrical」は日常的な場面で使われる気がします。
拡大図・縮図についての英語表現
拡大図と縮図は「元の形を変えずにサイズを変えた図形や図」のことです。
1.拡大図・縮図を英語で言うと…
まず、拡大することを「enlarge」や「scale up」、縮小することを「reduce」や「scale down」と言います。
このことから、拡大図は「enlarged diagram/ enlarged figures」、縮小図は「reduced diagram/ reduced figures」などと言えます。
どちらも「拡大された図」と「縮小された図」なので動詞は「受動態」となります。
2.拡大・縮小の「尺度」を英語で表すには?
拡大・縮小を考える上で重要なのが「尺度」です。
もとのサイズの何倍なのかを表すこの比率を「scale factor」と言います。
例えば次のような使い方ができます。
- For one triangle, the enlarged diagram with a scale factor of 2 has all the sides twice as long as each corresponding side of the original triangle.
(ある三角形について、その2倍の尺度の拡大図のすべての辺はそれに対応する元の三角形の辺の2倍になる) - If one quadrilateral is reduced by a factor of 1/2, the area of the reduced figure is a quarter of the area of the original figure.
(もしある四角形を1/2倍に縮小すると、その縮図の面積は元の面積の1/4になる)
「factor」は「第2章:倍数・約数・余りの英単語表現(中級・上級)」で「因数」と紹介しました。
この尺度の場面でも「scale factor」をもとの図に掛け合わせるということで同じです。
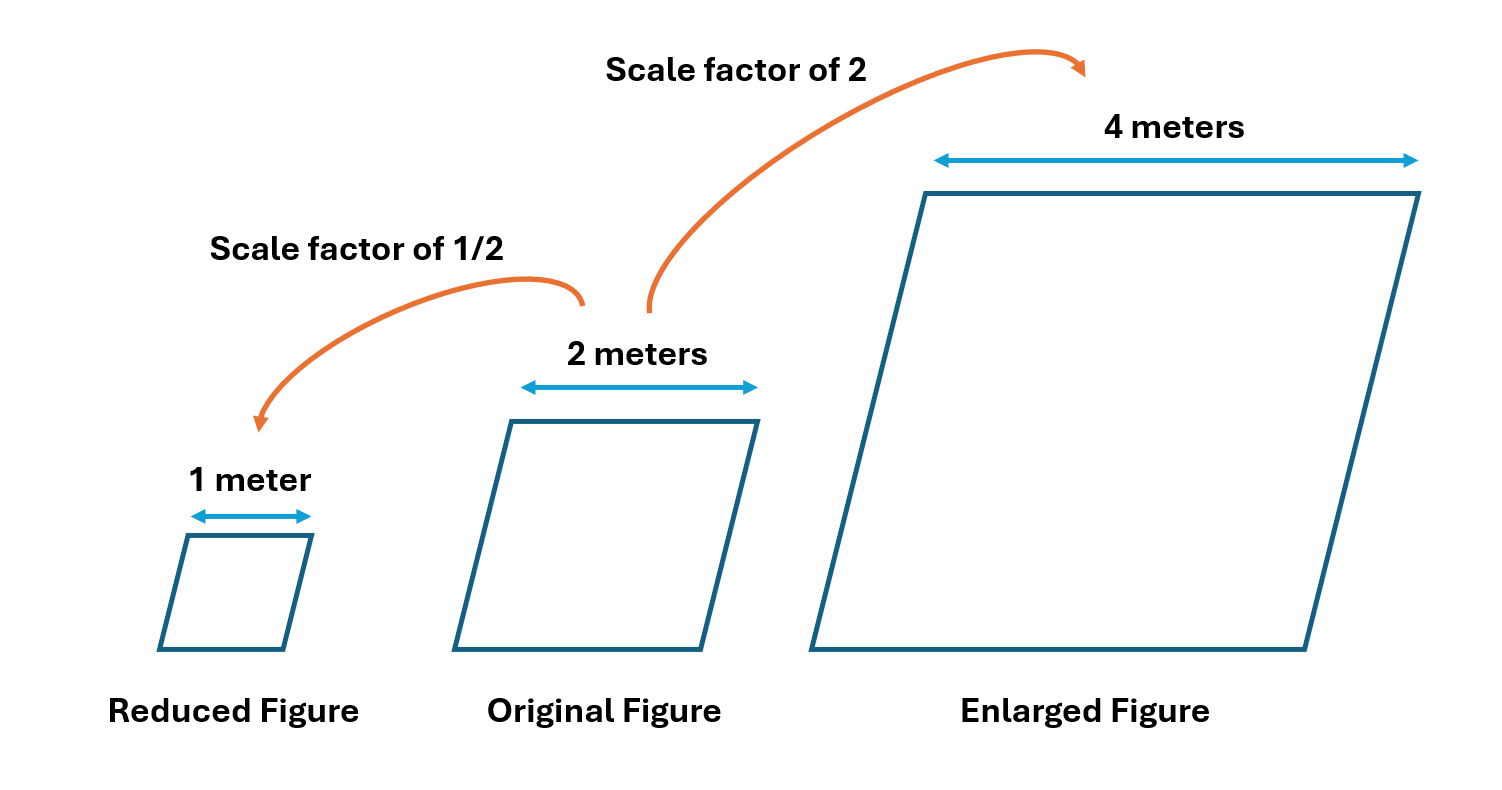
3.図を使ってより分かりやすく!
言葉だけだと分かりにくい部分もあると思います。
下の図を参考にしてください。
概形
次に、「概形」について話します。
1.概形とは?
私たちが日常的に見るような平面図形・立体図形は、三角形や直方体のように簡単ではなく面積や体積をもとめるのが非常に難しいです。
そんな時に使われるのが「概形」で「計算がしやすい簡単な図形に変換する」ということをします。
どのように、簡単な図形に変換するかは場面によって異なります。
次に出てくる図は、その一例です。
2.概形を英語で言うと…
英語で、概形は「approximate figure」や「approximate shape」と呼べます。
「第8章:概算と四捨五入の英語表現(初級)」で概算が「approximation」であったこととも関連しています。
下は楕円の概形を取った例です。
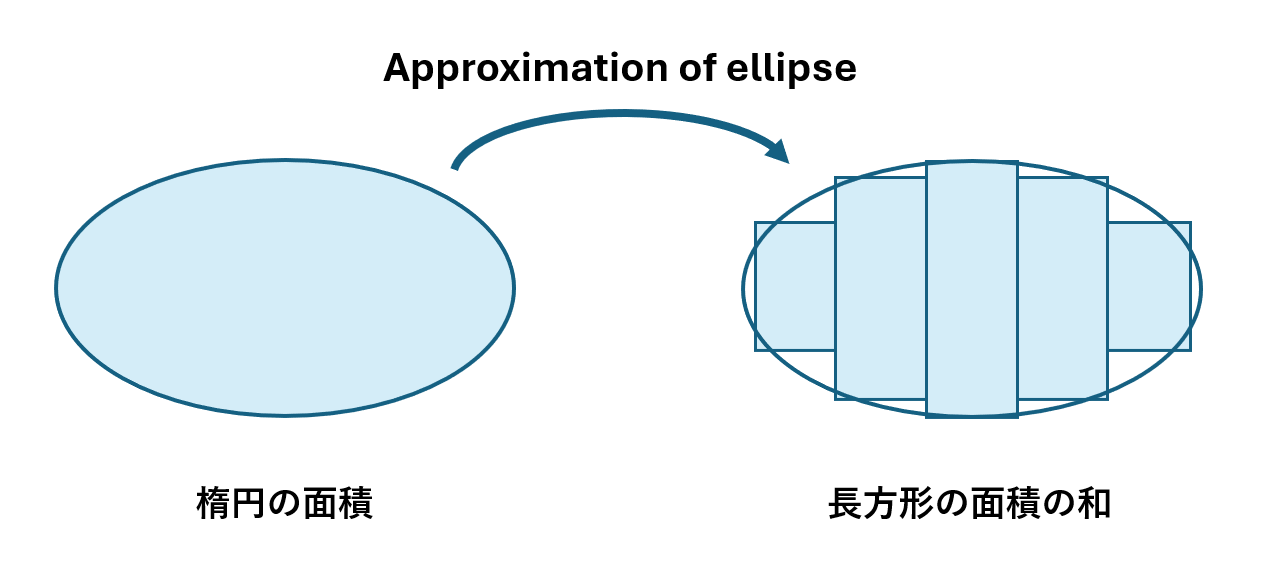
少し難しい話ですが高校で習う「積分」は「元の形の概形を取ることで面積を計算する一つの方法」です。
こんなところにも小学校の算数と高校の数学のつながりがあるんですね。
記事のまとめ
| 単語・表現 | 意味 |
|---|---|
| symmetry | 対称 |
| line symmetry | 線対称 |
| point symmetry | 点対称 |
| axis of symmetry, line of symmetry | 対称の軸 |
| point of symmetry, center of symmetry | 対称の点 |
| enlarged diagram, enlarged figures | 拡大図 |
| reduced diagram, reduced figures | 縮小図 |
| scale factor | 尺度 |
| approximate figure, approximate shape | 概形 |
最後に
いかがでしたか?
この章では、かなり多くの図形の性質を扱ったので一度に覚えるのが難しいかもしれません。この章の中で特に重要なのは、「平行と垂直」と「対称性」です。これらのセクションをまずは覚えましょう。
次の第14章では、「データの活用に必要な英語表現」を見ていきます。最後まで読んでいただきありがとうございました。




コメント