はじめに
こんにちは。イギリスの大学で数学を勉強しているゆーたです。
この記事では前回の続きとして、「正の数・負の数」についてさらに解説をしていきます。
特に、「負の数の入った四則演算(加減乗除)」について見ていきます。前回よりも内容は難しくなりますが、頑張りましょう。この記事の最後のセクションでは、「打ち消し合う・相殺する」という数学の操作についても解説しています。
ひとつ前の記事やこの後の記事について見たい方もいると思います。下のリンクからそれらの記事に飛んでください。
→ 正の数・負の数・数直線・絶対値とは?|正の数・負の数①
→ 負の数の入った四則演算を徹底解説!|正の数・負の数② ←現在の記事
→ 負の数の計算・分配法則・交換法則・結合法則|正の数・負の数③
→ 累乗・指数・負の数や分数の累乗をマスターしよう!|正の数・負の数④ 【近日公開!】
→ 自然数・素数・素因数分解をマスターしよう!|正の数・負の数⑤ 【近日公開!】
また以下の「英語編」の記事では、今回の記事に関わる英語の内容を解説しています。ぜひこちらも読んでみてください。
→ 英語で正負の数・数直線・絶対値は何という? (正の数・負の数-Part 1)
→ 英語で負の数の入った四則演算を表現しよう! (正の数・負の数-Part 2) 【近日公開!】
→ 英語で逆数・打ち消し合いを表現するには? (正の数・負の数-Part 3) 【近日公開!】
解説
簡単な用語の紹介
中学校では、これまで「足し算、引き算、かけ算、割り算」と呼んでいた四則演算をより数学的な名称で呼ぶようになります。
| 小学校 | 中学校 |
|---|---|
| 足し算 | 加法 |
| 引き算 | 減法 |
| かけ算 | 乗法 |
| 割り算 | 除法 |
また、中学数学からは「四則演算をした結果」についても特別な名前を付けることとします。
| 足し算(加法)の結果 | 和 |
| 引き算(減法)の結果 | 差 |
| かけ算(乗法)の結果 | 積 |
| 割り算(除法)の結果 | 商 |
例えば、「3×5=15」より、「15は3×5の積である」と言うことができます。

次のセクションからは、負の数のまじった四則演算について見ていきましょう。
学校や教科書での教え方と大きく異なるかもしれませんが、私が思う「もっともスムーズに理解できる方法」で説明したいと思います。
乗法(かけ算)
より分かりやすく説明するために、かけ算と割り算から先に解説します。
1.負の数の入ったかけ算の考え方
小学校までは、「正の数×正の数」を考えてきました。では、「負の数」が加わるとかけ算はどのようになるのでしょうか?
ここで、さっそく皆さんには次のルールを覚えてもらいます。このルールにより「積[かけ算の結果]の符号」が分かります。
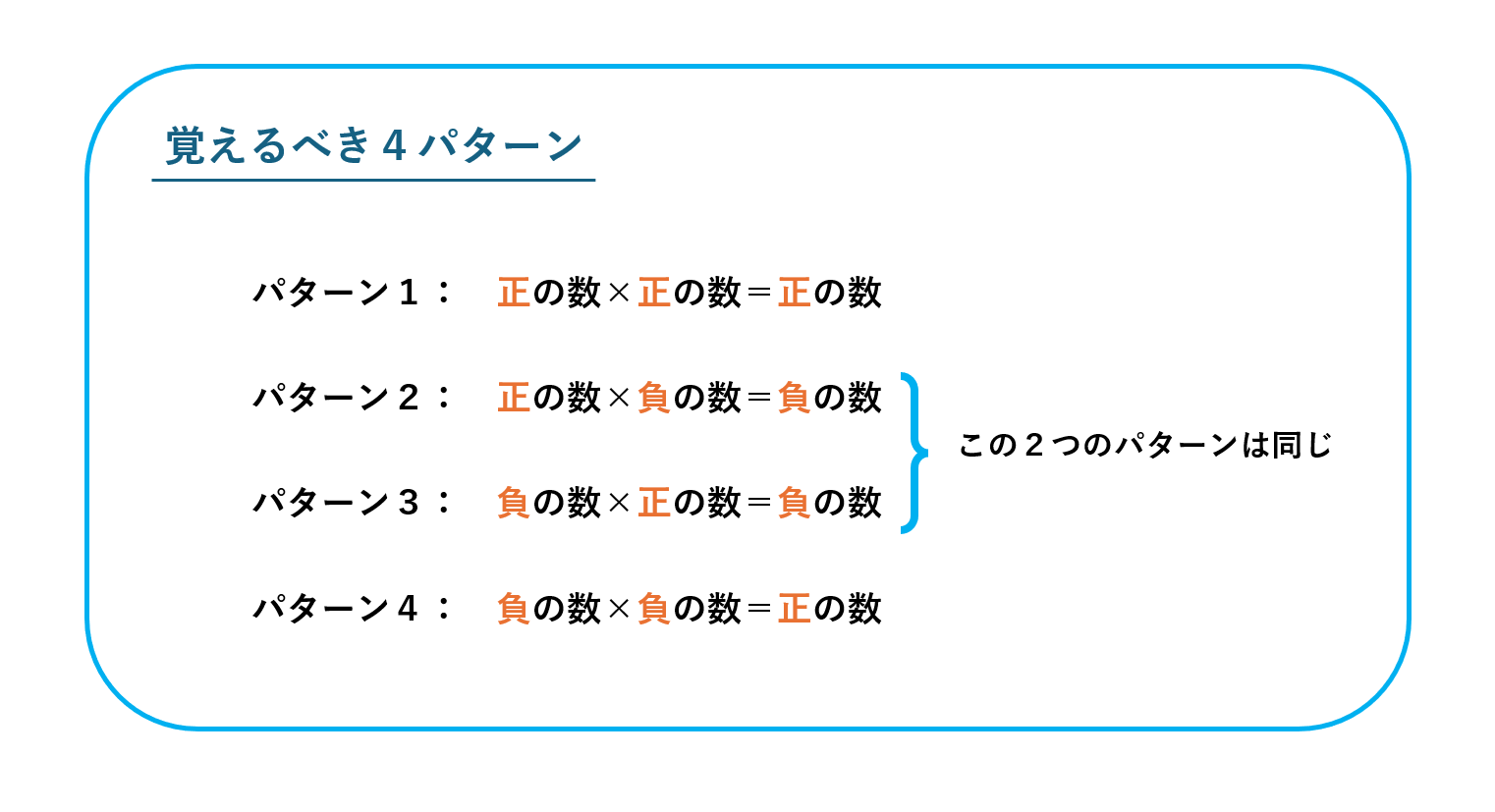
上のルールを使って積の符号が決定されます。符号以外の部分は「両方の数の符号を無視したかけ算(=絶対値のかけ算)」で計算できます。
2.上のルールを使った計算の例
では、下の例をもとにどのように計算されるのか見ていきましょう。
- $2\times3=6$
- $2\times(-3)=-6$
- $(-2)\times3=-6$
- $(-2)\times(-3)=6$
*かけ算・割り算のときは、「×ー」などとなると分かりにくいので負の数に()をつけます
正の数のかけ算とは異なり、「負の数が入ったかけ算は考えて仕組みが分かることはない」です。
「なぜこのようなルールになるのか?」と思う方もいるでしょう。しかし、その疑問に答えるには大学レベルの数学の理解が必要です。
中学数学では、「このルールを覚える」ことに集中しましょう。
3.かける数が増えた場合は?
3つの数のかけ算は、「まず2つの数のかけ算」をした後、「その積ともう1つの数」をかけて求めることができます。
\begin{align}
(-3)\times(-4)\times(-5) &=\{(-3)\times(-4)\}\times(-5) \\
&=(12)\times(-5) \\
&=-60
\end{align}
この例では、先に $(-3)\times(-4)$ を計算した後、その積 $12$ と一番右の $-5$ をかけ合わせています。
上の例で使われている波カッコは「優先して計算する」ことを表す方法です。
使い方については、次の記事の「四則の混じった正負の計算」のセクションで解説しています。
除法(割り算)
次に、割り算について見ていきましょう。
1.負の数の入った割り算の考え方
小学校では、「割り算は逆数を使ったかけ算」であることを習いました。例えば、「5÷3」は次のような関係でしたね。
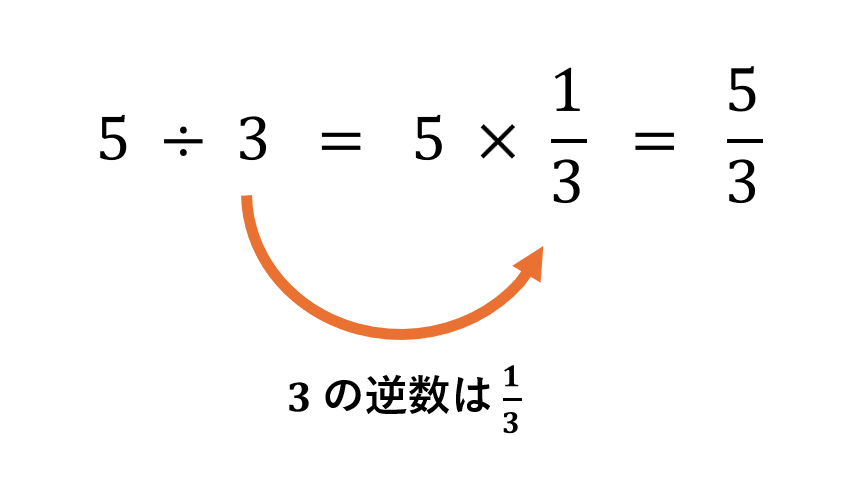
上の関係より、「負の数が入った割り算もかけ算の場合と同じ」ように計算できます。
負の数の場合も、逆数は「ある0でない数が与えられたときに、その数との積が1になる数」を表します。
よって、例えば「-5の逆数は$-\frac{1}{5}$」となります。ここで、負の数の逆数も負の数になることに注意しましょう。
2.上の考え方を使った計算の例
そうすると次のような計算ができます。
- $10\div(-2)=-5$
- $(-20)\div5=-4$
- $(-8)\div(-2)=4$
まだ慣れない場合には、一度「割る数を逆数に」した後計算するといいでしょう。
加法(足し算)と減法(引き算)
ここからは、負の数が入った足し算と引き算を見ていきます。
これらの計算を理解するために、次の2つのポイントに注目してもらいます。
ポイント1:負の数の範囲を意識した計算
皆さんは小学校で「5-2」を計算するときにどのようなことを考えていましたか?
一般的には、「5から2だけ取って、3が残る」という風に考えると思います。
では、「5-8」はどうしますか?
「5からは5以上取れない」ですよね。
この考えを変える必要があります。
今の私たちは「負の範囲」を考えられます。
これを目で見て分かるようにするのが前回学習した「数直線」です。
数直線上で、「5-2」を次のように考えましょう。
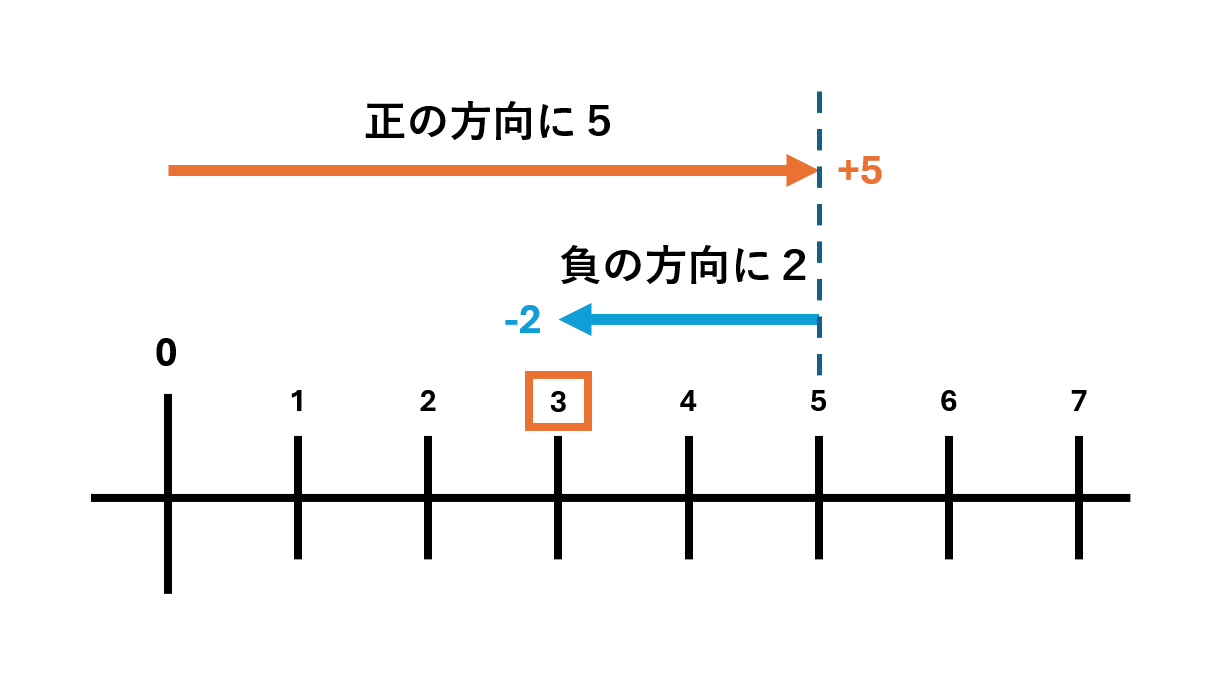
この図から、
であることがわかると思います。
同じ考え方で「4-7」についても考えてみましょう。
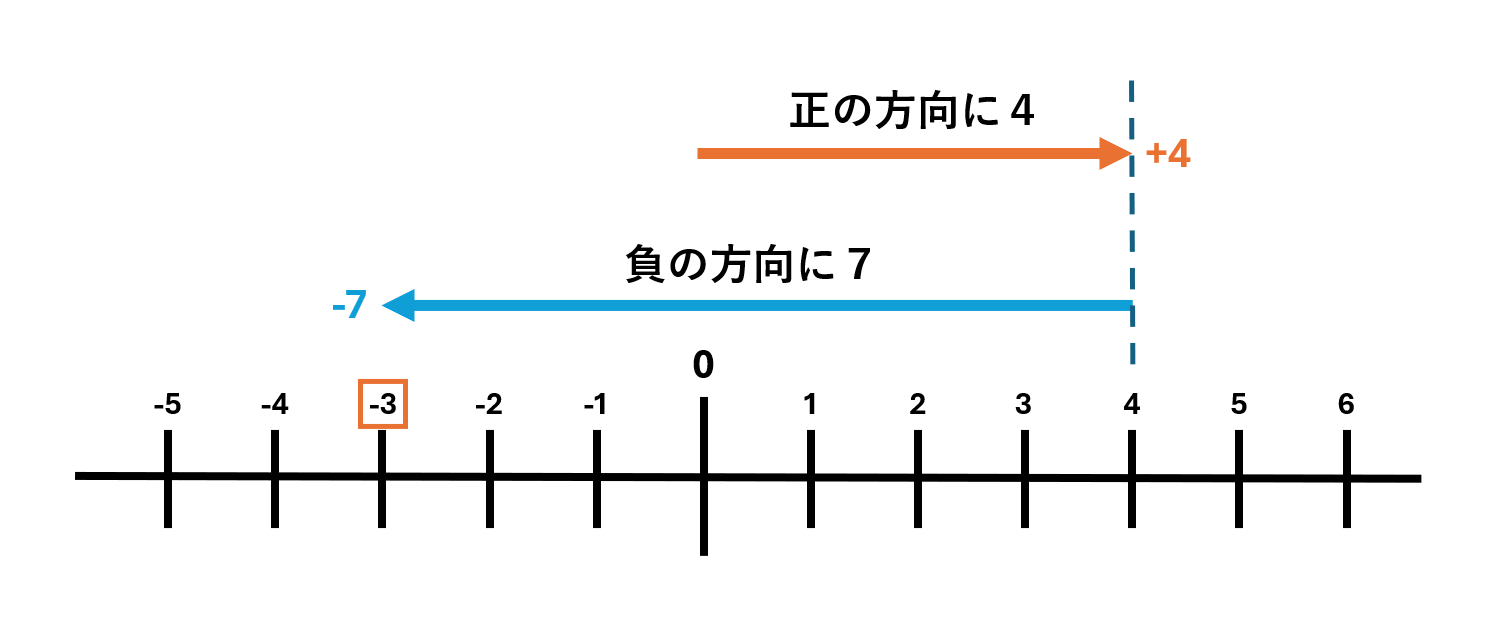
これを見ると、計算の結果は「-3」で「負の範囲」にあることがわかると思います。
上の考え方が理解できれば、次のような計算も簡単にできるでしょう。
- $-8+5=-3$
- $-4+(-6)=-4-6=-10$
ポイント2:負の数の引き算は足し算
数直線を使うことでほとんどの足し算・引き算は理解することができました。
しかし、次のような「負の数の引き算」はどうでしょう?
$3-(-1)$ $-2-(-6)$
これを考えるには、計算式を次のように見るといいでしょう。
$3-(-1)=3+\color{red}{(-1)\times(-1)}$ $-2+\color{red}{(-1)\times(-6)}$
こうすることで、先ほどのかけ算のルールより、 $(-1)\times(-1)=1$、 $(-1)\times(-6)=6$ となります。
すると、この計算は普通の足し算になるというわけです。
「負の数の引き算は足し算になる」という事実はここで覚えてしまいましょう。
打ち消し合う/相殺するとは
最後に、「打ち消し合う/相殺する」という言葉の使い方を説明します。
1.掛け算で使われる「打ち消し合う」の意味
ある数にその数の逆数をかけたとき「打ち消し合う」もしくは「相殺する」と言います。
例えば…
$5\times{\frac{1}{5}}=1$
という計算は「5とその逆数 $\frac{1}{5}$ が打ち消し合う/相殺される」などと表現されます。
2.足し算・引き算で使われる「打ち消し合う」の意味
「打ち消し合う/相殺する」という表現は、足し算・引き算についても使えます。
足し算・引き算の場合には、「計算の結果が0になること」を指します。
例えば…
$5+(-5)=0$
という計算は「5と-5が打ち消し合う/相殺される」などと表現されます。
最後に
いかがでしたか?「加→減→乗→除」の順番で習うのが一般的だと思いますが、今回は「乗→除→加→減」の順番に変えて解説していきました。
この解説などについての感想なども教えていただけると嬉しいです。
また以下の「英語編」の記事では、今回の記事に関わる英語の内容を解説しています。
ぜひこちらも読んでみてください。
→ 英語で正負の数・数直線・絶対値は何という? (正の数・負の数-Part 1)
→ 英語で負の数の入った四則演算を表現しよう! (正の数・負の数-Part 2) 【近日公開】
→ 英語で逆数・打ち消し合いを表現するには? (正の数・負の数-Part 3) 【近日公開!】




コメント