はじめに
本記事では、初級に引き続き「データの活用に必要な英語表現」を紹介します。今回は、小学校５・６年で習ったグラフや表などに関する表現や単語を解説します。初級に比べて扱う内容が難しくなるので、その分英単語の難易度も上がります。頑張っていきましょう。
また、初級の内容をまだ読んでいない方や、データ分析に関する英語表現を解説した上級の記事を読みたい方は下のリンクから飛んでください。
→ データの活用に必要な英語表現（初級）
→ データの活用に必要な英語表現（上級）
（所要時間：１０分）
単語・表現の一覧
| 単語・表現 | 意味 |
|---|---|
| pie chart, pie graph | 円グラフ |
| ratio | 比 |
| proportion | 全体に対する部分の割合 |
| percentage | パーセント、比率、百分率 |
| bar chart (もしくは horizontal bar chart) | 帯グラフ |
| stacked bar chart, composite bar chart | （全体のサイズを比較できる）複数の帯グラフ |
| average | 平均 |
| true value | 真の値 |
| error | 誤差 |
| representative value | 代表値 |
| mean value, mean | 平均値 |
| median | 中央値 |
| mode | 最頻値 |
| dot plot, dot chart | ドットプロット |
| frequency distribution | 度数分布 |
| class | 階級 |
| frequency | 度数 |
| class width, class interval | 階級の幅 |
| frequency distribution table | 度数分布表 |
| greater than or equal to A but less than B | A以上B未満 |
| histogram | 柱状グラフ |
単語の解説
５年生：円グラフ、帯グラフ、測定値の平均
１．円グラフと帯グラフ
円グラフは「円を扇形に分割することで全体に対するあるもの比率を表すグラフ」です。
これは英語では「pie chart」もしくは「pie graph」と呼ばれます。
その理由は円グラフがアップルパイのようなパイに似ているからです。
円グラフの最も大きな特徴は「比率や割合を表すことができること」です。
英語で比率や割合を表すのに使われるのが「ratio」や「proportion」、「percentage」です。
「ratio」は「比を表し、２つの数量の比率を表すとき」に使われます。
また、「proportion」は「全体に対する部分の割合」を表します。
「percentage」はそのままですね。
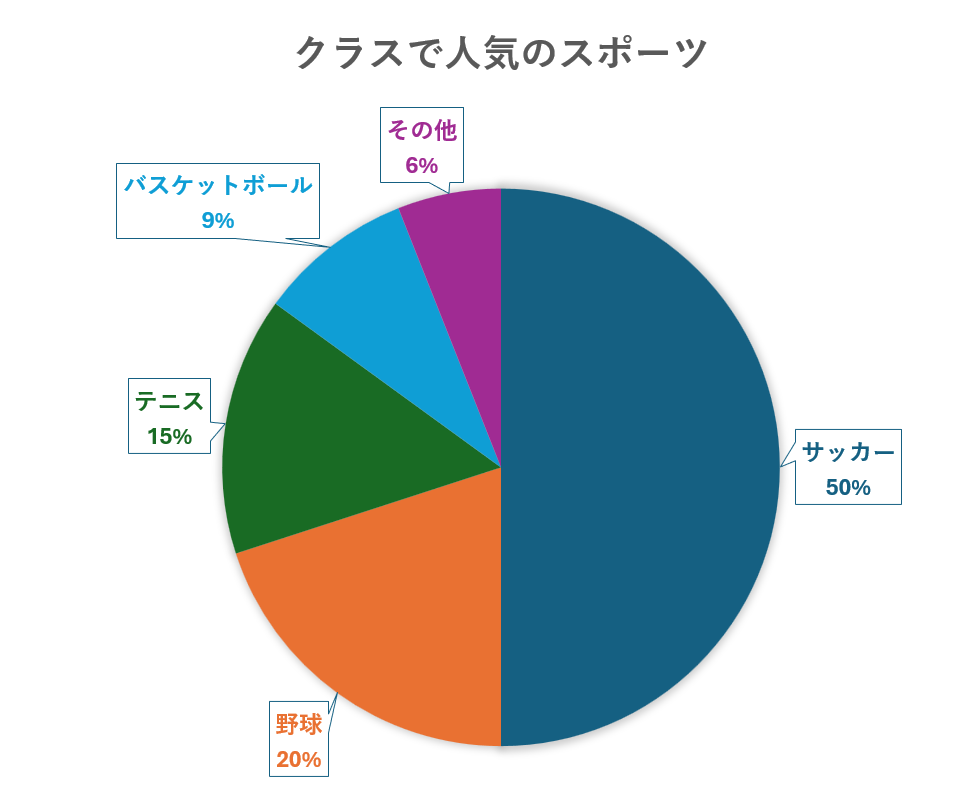
上の円グラフを使って次のような例文が作れます。
- The ratio of students who chose “soccer” to “basketball” is 5 to 2 (5:2). （野球に対してサッカーを選んだ学生の比は５対２である５
- The proportion of students who chose “baseball” is 20%. （野球を選んだ学生の割合は２０％である）
- The percentage of students who chose “tennis” is 15%. （テニスを選んだ学生の割合は１５％である）
また、円グラフと同様に「全体に占める割合」を表すことができるグラフに「帯グラフ」があります。
帯グラフは長方形を割合に対応させていくつかに区切ったような形のグラフです。
帯グラフは「bar chart」の一種として認識されているのでこれも「bar chart」と言われます。
区別するために棒グラフを「vertical bar chart」、帯グラフを「horizontal bar chart」とするといいでしょう。
また、帯グラフが円グラフと違うところは「全体のサイズを比較することができること」です。
下の例のように、円グラフでは表現しづらいデータの全体数の違いを帯グラフはうまく表現できています。
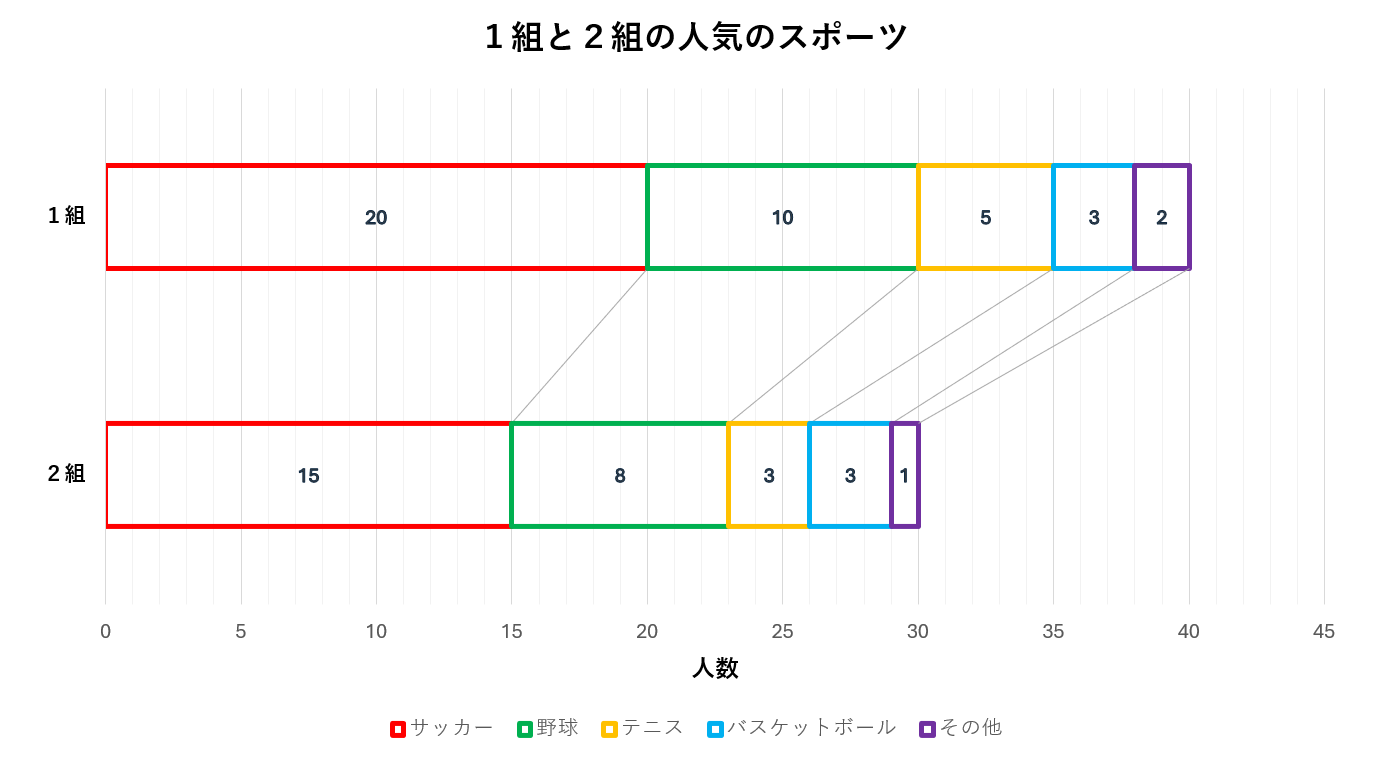
このように、複数の帯グラフがある場合には「stacked bar chart」もしくは「composite bar chart」と呼ばれます。
「stacked」は「積み重なった」、「composite」は「複合した」という意味です。
２．測定値の平均
小学５年生で習うもう一つのトッピクは「平均」です。
平均を計算する一つの目的は、「自分が測定した値を真の値に近づけること」です。
これを英語では平均を「average」、真の値「true value」と言います。
- The true average height of all male students in the class is 162 cm, whereas the average height of three male students in the class is 160 cm. （クラスの男子生徒全体での実際の平均身長は162cmなのに対して、クラスの中のある３人の男子生徒の身長の平均は160 cmである）
＊この例文では「true value」が「true average height」となっており、「average」と「true value」の両方が1つになった表現になっています。
この平均を求める過程で重要になるのが「誤差、測定の誤り」です。
誤差は英語で「error」と言います。
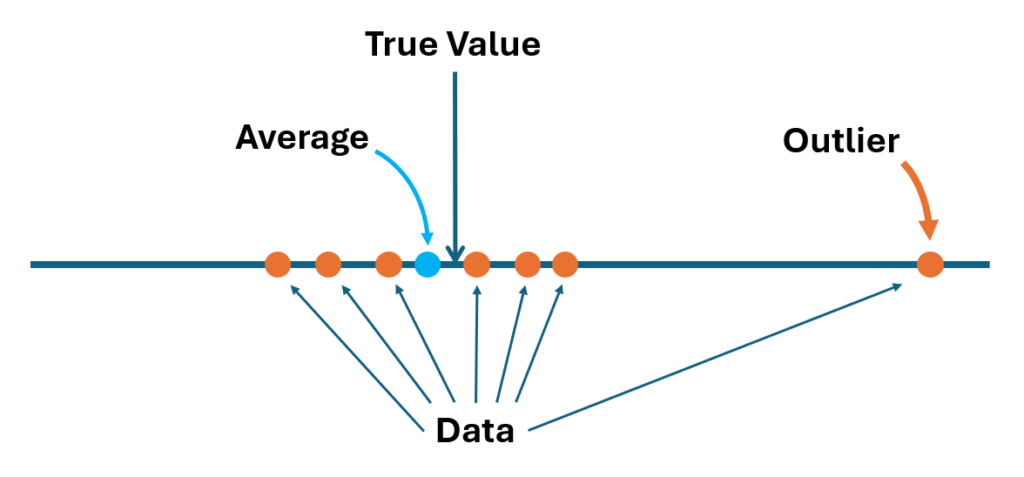
特に、誤差を大きくするような他の値と大きくずれた測定値を「外れ値」と呼びます。
これを英語では「outlier」と言います。
語源は「out（離れて）」と「lier（横たわる人・もの）」が一つになってできた単語です。
「うそつき」を意味する「liar」と間違えないようにしましょう。
６年生：代表値、度数分布
１．代表値とドットプロット
代表値とは「収集したデータ全体の様子や特徴を一つの数値で代表させて表そうとする場合に使われる数値」です。
小学校では、代表値として「平均値」と「中央値」、「最頻値」を習いました。
| 種類 | 意味 |
|---|---|
| 平均値 | データ全体の和をそれらのデータの数で割った値、平均のこと |
| 中央値 | データを大きさの順に並べた場合の真ん中の値 |
| 最頻値 | すべてのデータの中で最も多く出てくる値 |
代表値は英語で「representative value」、平均値は「mean value」もしくは「mean」、中央値は「median」、最頻値は「mode」と言います。
「representative」は「代表する、代表的な」という意味の形容詞です。
平均は「average」でしたが、平均値は「mean」であることに注意しましょう。
「median」という単語はなんとなく「真ん中」を意味しているのが分かると思いますが、「mean」と「mode」はどうでしょう？
これらの語源はどちらもラテン語と関係しています。
「mean」はラテン語で「medianus（中間）」という単語から「中間的な値＝平均値」となりました。
実は「median」も「medianus」から来た言葉ですが、言語の発展・細分化の過程で異なる言葉となりました。
また、「mode」の語源はラテン語の「modus（基準、測定）」から来ており、最頻値という意味に発展しました。音楽でも「音階、調」を意味する「mode」がありますがこれも同じ語源です。
さらに、小学6年生では代表値の意味や関連性を考えるために「ドットプロット」と呼ばれるグラフを使用しました。
これを英語では「dot plot」もしくは「dot chart」と呼びます。
注意点として、点の数が複数でも「dot plot of 20 values」のように「plot」は単数のままです。
下の図は「直近16試合のゴール数」をドットプロットで表した例です。
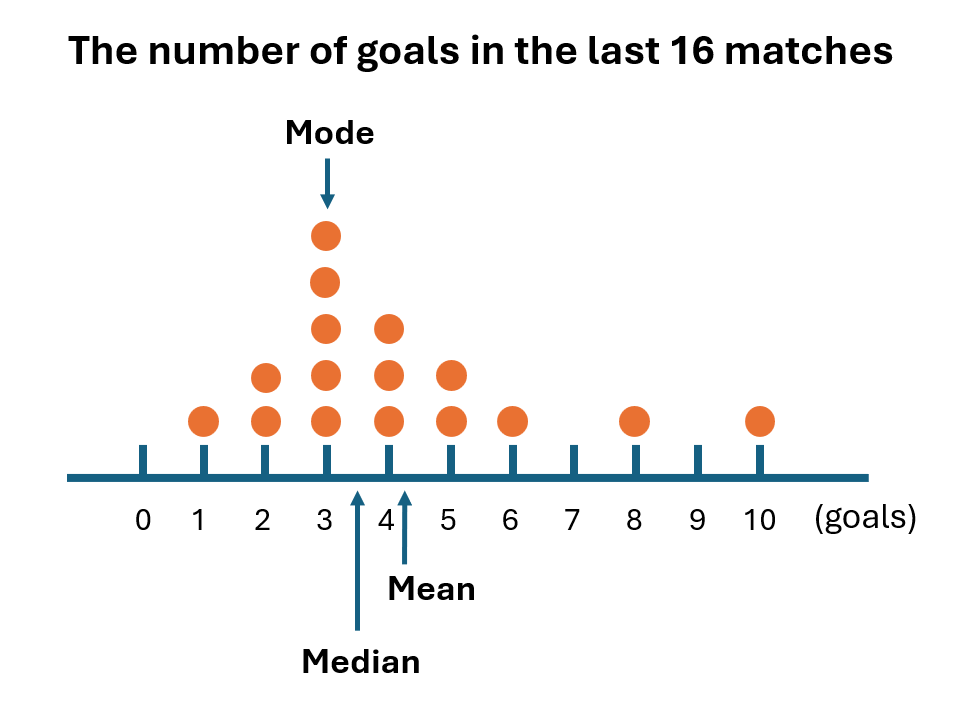
ここで言うドットプロットは、散布図の一種である別の意味でのドットプロットとは違います。
ちなみに、その意味でのドットプロットは「cleveland dot plot」と呼ばれるそうです。
２．度数分布を表す表やグラフ
まず、度数分布とは「測定したデータをいくつかの区間に分けることで、全体の特徴を読み取りやすくする方法」です。
例えば、あるクラスの身長を測定した場合に、身長の範囲を１０cmごとに分けることで、それぞれの区間に入る人数を表などにまとめることができる。
この場合の区間のことを「階級」、それぞれの区間に入る数値の個数のことを「度数」と呼びました。
英語で度数分布は「frequency distribution」、階級は「class」、度数は「frequency」と言います。
また、それぞれの階級の幅は「class width」や「class interval」と呼びます。
度数分布という言葉は日本語でもほとんど使わないですが、「distribution（分布）」という言葉は今後も出てくるので覚えてもいいと思います。
小学６年生で習う度数分布を表す方法には「度数分布を表す表（度数分布表）」と「柱状グラフ」があります。
度数分布表は英語で「frequency distribution table」と呼ばれます。
以下がその一例です。
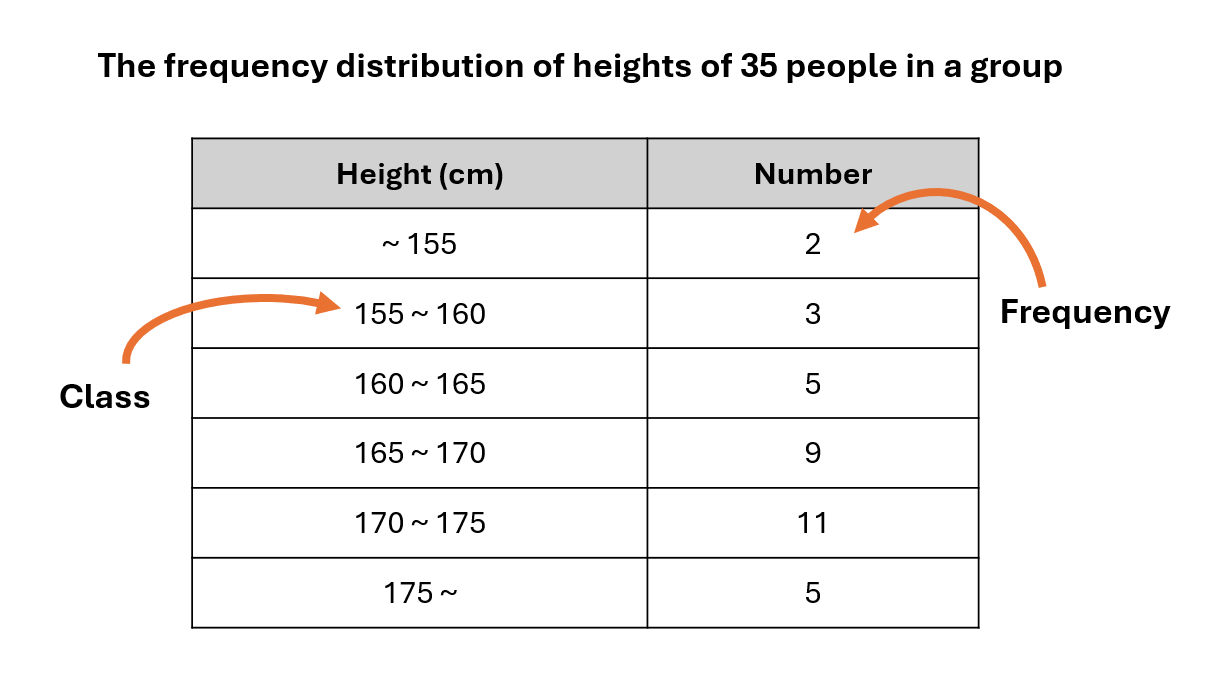
上の表での「~」は「A以上B未満」を表しています。
英語では「greater than or equal to A but less than B」と言えます。
また、柱状グラフは「histogram」と呼ばれます。
柱状グラフの横軸はデータの数値が表され、それを階級ごとに分けた形になっています。
小学３年生で習った棒グラフとは縦軸と横軸の表すものが異なるので、同じものと考えないように気を付けましょう。
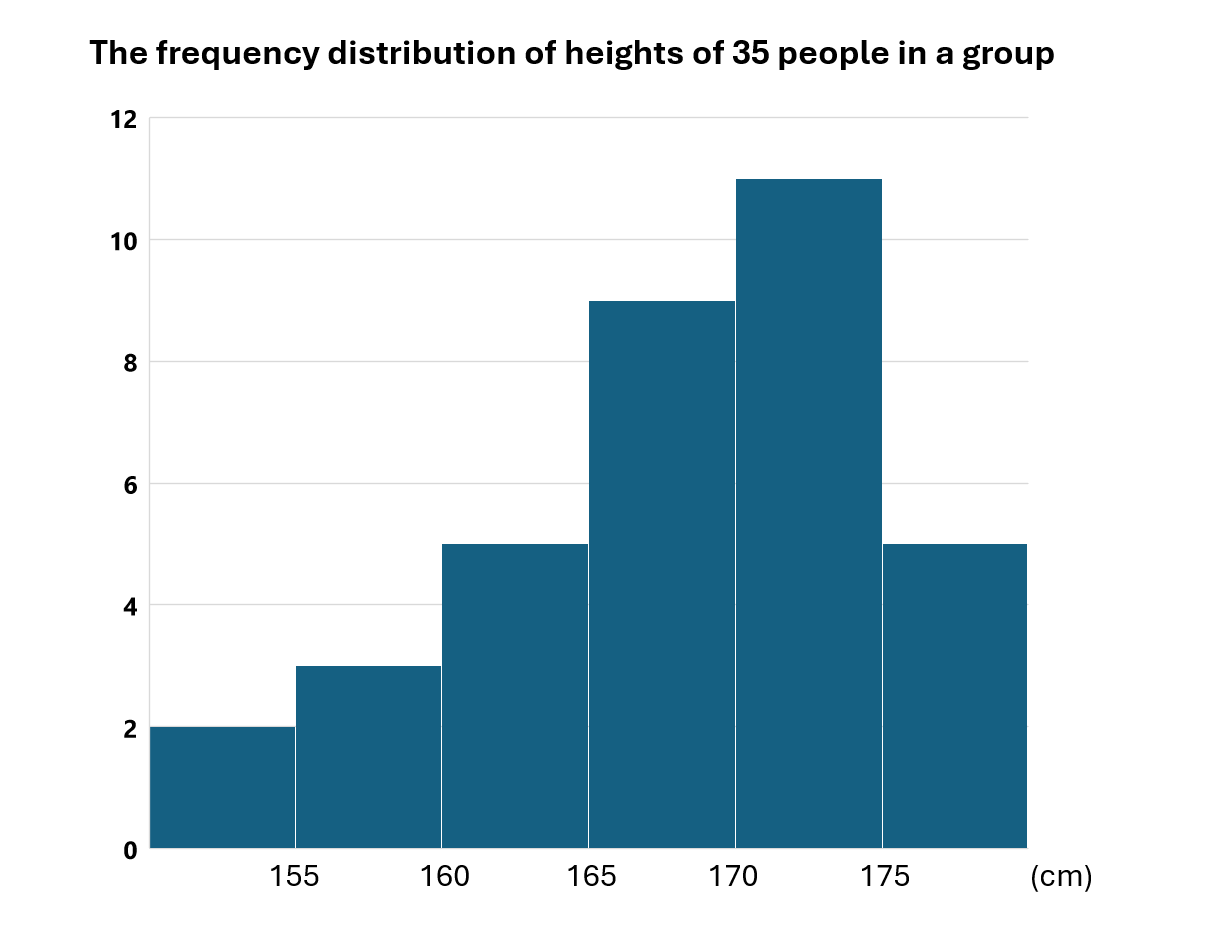
柱状グラフについて詳しく調べるのは中学生の範囲ですが、その分布の形を簡単に分析をすることはできます。
例えば、左右の広がりの範囲「spread (or width) of distribution」や度数がもっとも高い範囲「modal class (class with the highest frequency) 」、対称性「symmetry」などがあげられます。
先ほど紹介した最頻値は「度数がもっとも高い値」と表現できるので、度数がもっとも高い範囲について「modal」という言葉が使えます。
記事のまとめ
| 単語・表現 | 意味 |
|---|---|
| pie chart, pie graph | 円グラフ |
| ratio | 比 |
| proportion | 全体に対する部分の割合 |
| percentage | パーセント、比率、百分率 |
| bar chart (もしくは horizontal bar chart) | 帯グラフ |
| stacked bar chart, composite bar chart | （全体のサイズを比較できる）複数の帯グラフ |
| average | 平均 |
| true value | 真の値 |
| error | 誤差 |
| representative value | 代表値 |
| mean value, mean | 平均値 |
| median | 中央値 |
| mode | 最頻値 |
| dot plot, dot chart | ドットプロット |
| frequency distribution | 度数分布 |
| class | 階級 |
| frequency | 度数 |
| class width, class interval | 階級の幅 |
| frequency distribution table | 度数分布表 |
| greater than or equal to A but less than B | A以上B未満 |
| histogram | 柱状グラフ |
最後に
今回の記事はいかがでしたか？
内容によっては難しいと感じるものも含まれていたかもしれません。ここまでの内容で小学校で習う範囲のデータの活用に関する表現はカバーしました。上級ではここまでの内容を生かして、簡単な英語での分析の仕方を紹介します。興味のある方は上級も読んでみてください。最後まで読んでいただきありがとうございました。
コメント