はじめに
この記事では、第13章として「図形で習ういろいろな性質」について解説します。この章は、初級と中級の記事に分かれています。小学校で習った図形の性質として、「平行・垂直」や「図形の合同」などを順番に説明していきます。
また今回の内容は、第11章と第12章の内容と関連しています。以下のリンクより一緒に読んでおくと、理解がより深まると思います。
→ 第11章:平面図形の特徴と種類(初級)
→ 第12章:立体図形の特徴と種類(初級)
(所要時間:10分)
単語・表現の一覧
| 単語・表現 | 意味 |
|---|---|
| parallel | 平行 |
| perpendicular, orthogonal, normal | 垂直 |
| horizontal | 水平 |
| vertical | 鉛直 |
| congruence | 合同 |
| incongruence | 合同でない |
| corresponding side | 対応する辺 |
| corresponding angle | 対応する角 |
| corresponding vertex | 対応する頂点 |
単語の解説
平行と垂直についての英語表現
図形を習ううえで必ず出てくるのが「平行と垂直」です。
1.平行と垂直を英語で言うと…
平行を表す単語には「parallel」、垂直を表す単語には「perpendicular」、「orthogonal」、「normal」があります。
ただ基本的には「parallel」と「perpendicular」を覚えればいいでしょう。
| 単語 | 意味 |
|---|---|
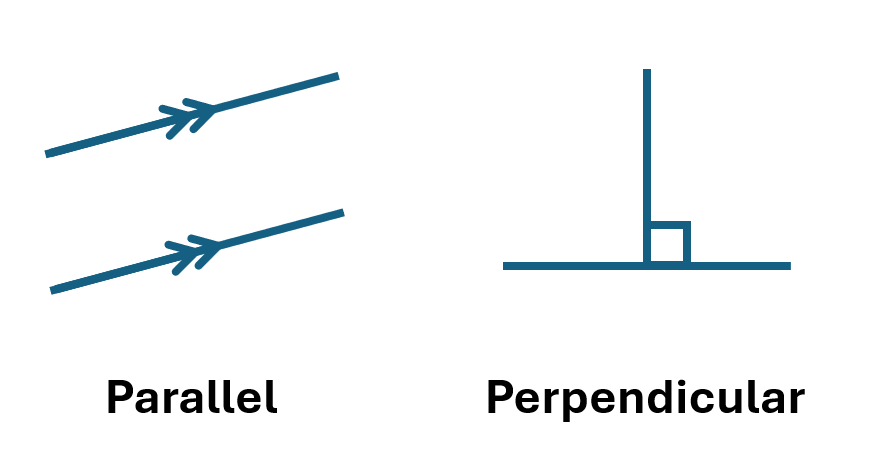
| parallel | 平行(二直線が永遠に交わらない状態) |
| perpendicular | 垂直(二つの線が直角で交わる状態) |
高校までのレベルでは「orthogonal」という単語は「perpendicular」と同じ意味と考えていいと思います。
また、「normal」という単語も高校や大学までは使わない単語なので重要度は低いです。
2.平行・垂直の英語表現を使った例文
では上の表現を使った例文を紹介します。
- The straight-line AB is parallel to the straight-line CD.
(直線ABは直線CDと平行である) - The straight-line AB is perpendicular to the straight-line CD.
(直線ABは直線CDと垂直である)
3.水平・鉛直の意味の確認
平行・垂直と似た考え方に「水平・鉛直」があります。
念のため、これらの意味を一度確認しましょう。
| 用語 | 意味 |
|---|---|
| 水平 | 重力の向きに直交する状態 |
| 鉛直 | 重力の向きと同じ方向を表す状態 |
4.水平・鉛直を英語で言うと…
水平は「horizontal」、鉛直は「vertical」と表すことができます。
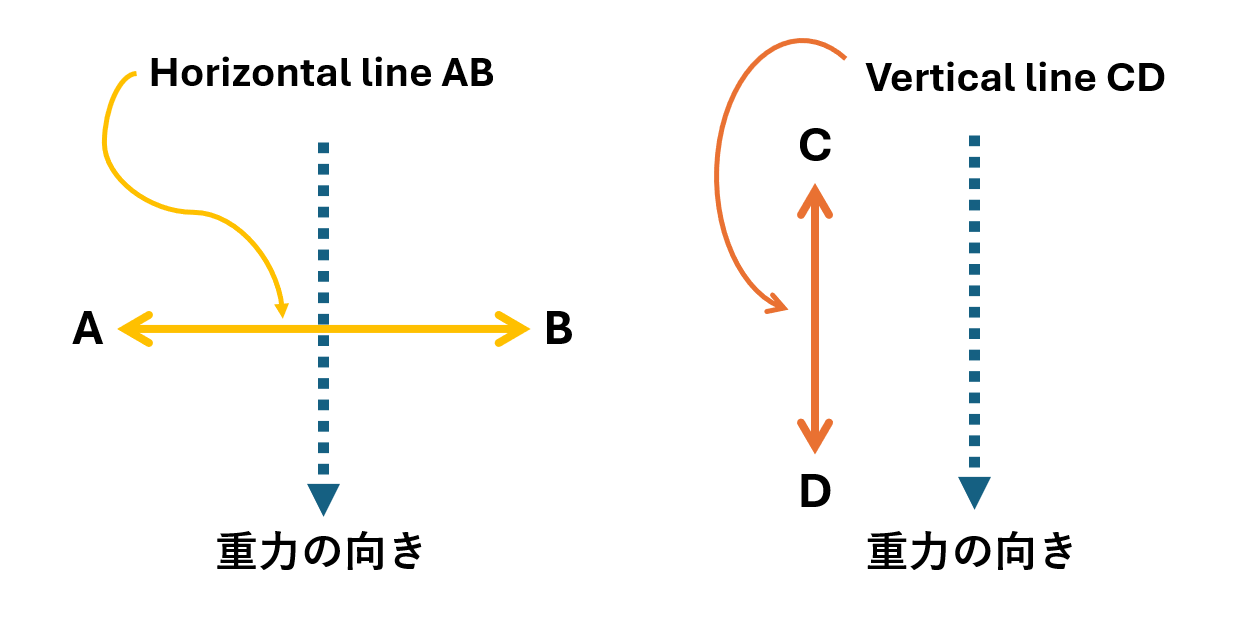
- Any horizontal line is perpendicular to any vertical line.
(どの水平な線も鉛直な線に垂直である)
例文の意味は、次の図を想像すれば分かりやすくなるかもしれません。
5.「perpendicular」と「vertical」の違い
注意点として「perpendicular」と「vertical」は同じ意味の単語ではありません。
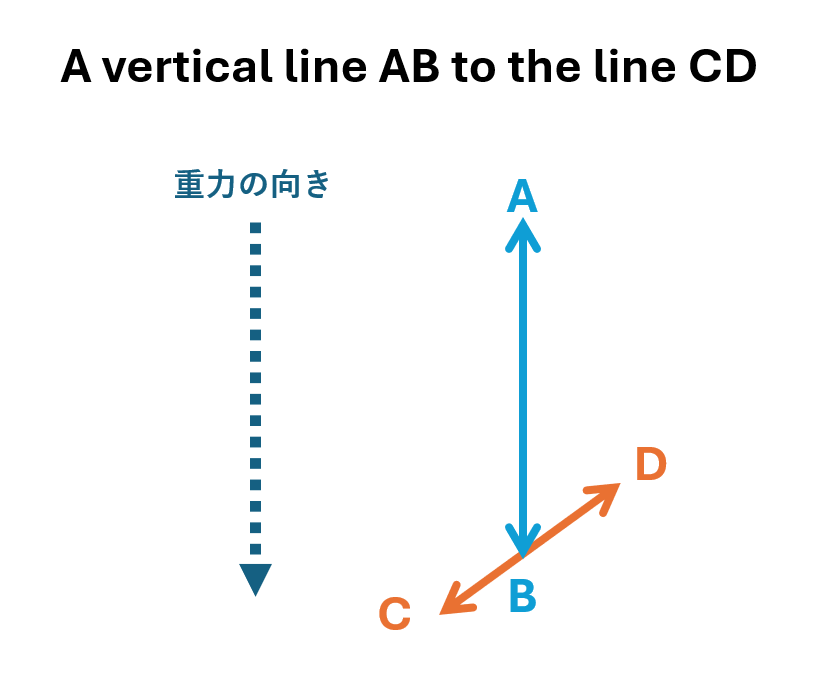
「perpendicular」は「二つの直線が直角で交わる状態」ですが、「vertical」は「重力の向きと同じなだけ」です。
なので、「Draw a vertical line AB to the line CD」と言われても「直線ABと直線CDが直角で交わる必要はない」のです。
図形の合同についての英語表現
1.合同の意味の確認
まず、図形の合同の意味について確認しましょう。
2つの図形が合同であるとは「それらの図形の形と大きさが同じであること」です。
また、平面図形をひっくり返してもう一つの図形に重なるようなものも合同であると言えます。
このひっくり返して重なるような図形は英語で「the mirror image of the obejct」などと呼ばれます。
「mirror」とは「鏡」のことで、「鏡に映された図形」を指しています。
2.合同を英語で言うと…
英語では合同を「congruence」と言います。
逆に、合同でないことを「incongruence」と言います。
この単語は日常会話で使われない上に難しい単語なので、中学・高校の段階では覚える必要がないと思います。
また、日本では合同を小学校で習いますが他の国では中学くらいまで習わないと思います。
中学数学の「相似」という単元でもう一度紹介するのでそのときに覚えてくれればいいです。
3.「congruent」の意味と例文
「congruent」を使うと、「合同な図形」や「2つの図形は合同である」などと言うことができます。
では、例文を見てみましょう。
- Two quadrilaterals are congruent.
(二つの四角形は合同である) - Triangle ABC is congruent with triangle DEF.
(三角形ABC は三角形DEF と合同である) - Congruent figures.
(合同な図形) - This plane figure is not congruent to any other figures.
(この平面図形は他のどの図形とも合同でない)
4.合同に関連する英語表現とその例文
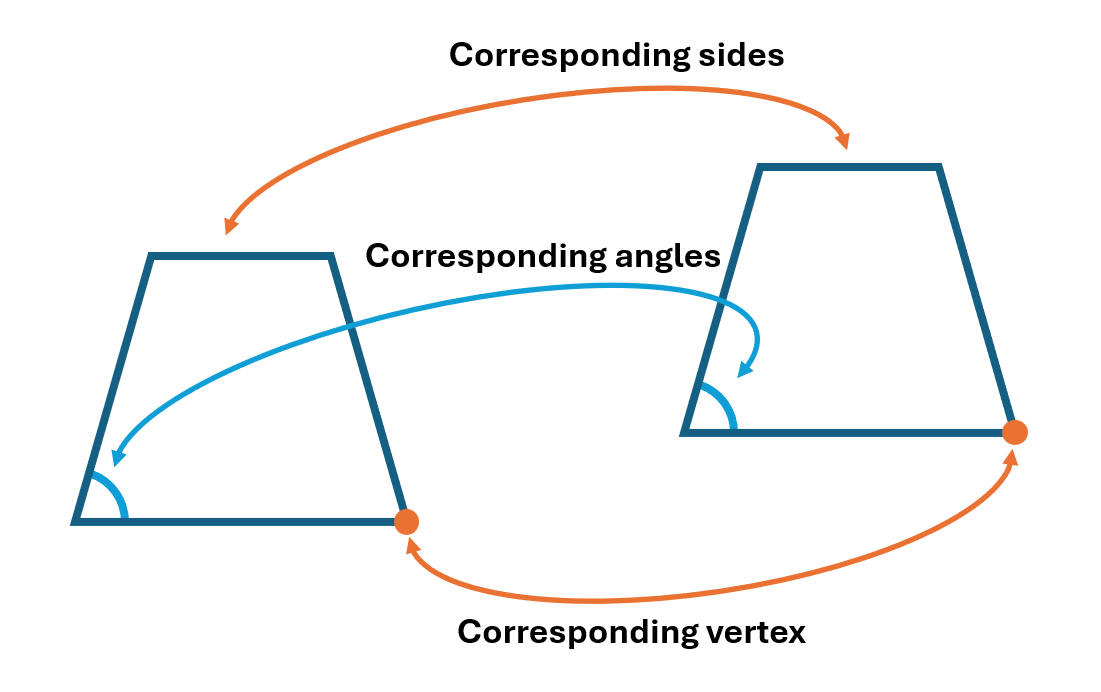
小学校で合同を考えるときは「対応する辺」と「対応する角」、「対応する頂点」を考えました。
これを英語では「corresponding side」と「corresponding angle」、「corresponding vertex」と言います。
図も載せておきます。
これらの表現を使った例文を見ましょう。
- If two triangles are congruent, each side of one triangle has the corresponding side of another triangle.
(もし2つの三角形が合同なら、1つの三角形の辺はそれに対応する辺をもう1つの三角形に持つ) - The corresponding angles are always equal for any congruent figures.
(どの合同な図形も対応する角の大きさは等しい)
二つ目の例文のように、「対応する角」が両方の図形の角を指す場合には複数形となります。
5.海外で合同を記号で表すには?
最後に合同を表す記号を紹介します。
日本では三本線を使った「≡」の記号が使われます。
しかし、日本以外のほとんどの国では「≅(等号の上に波線が一本入った記号)」が使われる場合が多いです。
複雑な記号になると複数の意味を持つ場合が多くあります。
そうすると、合同の記号のように国によって異なる場合もよくあります。
記事のまとめ
| 単語・表現 | 意味 |
|---|---|
| parallel | 平行 |
| perpendicular, orthogonal, normal | 垂直 |
| horizontal | 水平 |
| vertical | 鉛直 |
| congruence | 合同 |
| incongruence | 合同でない |
| corresponding side | 対応する辺 |
| corresponding angle | 対応する角 |
| corresponding vertex | 対応する頂点 |
最後に
いかがでしたか?
この後の中級では、「対称性」と「拡大図・縮図と概形」について見ていきます。
見慣れない表現も多いと思いますが、楽しんで読んでください。
この記事を最後まで読んでいただきありがとうございました。




コメント