はじめに
本記事では、初級の記事に引き続き「分数」に関する英語表現を解説していきます。
小学5・6年生でならう分数の話の中には「通分・約分・逆数」があったと思います。これらは分数の単元の中でも必ず押さえなければいけない内容です。これらの関係性などについても意識しながら英語での表現の仕方を見ていきましょう。
初級をまだ読んでいない方や、上級の記事も読みたい方は以下のリンクから飛んでください。
→ 分数の英語表現（初級）
→ 分数の英語表現（上級）
（所要時間：５～１０分）
単語・表現の一覧
| 単語・表現 | 意味 |
|---|---|
| reducing fractions | 約分 |
| simplifying fractions | 約分 |
| reduce A to B | A を B に約分する |
| simplify A to B | A を B に約分する |
| reduce to its lowest terms | 既約分数にする |
| （分数に対して言うときの）terms | 分母と分子の両方を指す単語 |
| reducing the fractions to a common denominator | 通分 |
| common denominator | 共通分母 |
| the least common denominator | 最小の共通分母 |
| the lowest common denominator | 最小の共通分母 |
| unlike fractions (もしくは fractions with different denominators) | 分母の異なる２つ以上の分数 |
| reciprocal | 逆数 |
| (multiplicative) inverse | 逆数 |
単語の解説
約分について
約分とは「分数の分母と分子を公約数で割ってより簡単な分数にすること」でした。
まず、約分は英語で「reducing fractions」もしくは「simplifying fractions」と表されます。
同じように、「A を B に約分する」は「reduce A to B」もしくは「simplify A to B」となります。
また、「第２章：倍数・約数・余りの英語表現（初級）」で紹介しましたが、公約数は「common divisor」もしくは「common factor」、その中で最大のものを指す最大公約数は「the greatest common divisor」と言いました。
「第２章：倍数・約数・余りの英単語表現（中級・上級）」で言及した通り、約数という意味での「divisor」と因数という意味での「factor」は、どちらを使用しても同じ意味になります。
ただ、最大公約数と言うときには「divisor」の方を使うのが一般的です。
では、これらを使った例文を見てみましょう。
- We can reduce 2/4 to 1/2 by the common factor 2. （2/4 は公約数２で、1/2 に約分できる）
- 7/21 is reduced to 1/3. （7/21 は 1/3 に約分される）
- The greatest common divisor of the numerator and the denominator in the above case is 7. （上の場合の分子と分母の最大公約数は７である）
そして、最大公約数で約分された分数は「既約分数」と呼ばれますが、分数が既約分数であることを次のように表します：
以下はすべて同じ意味の文章です
- 1/5 is irreducible. （1/5 は約分できない）
- 1/5 is reduced. （1/5 は約分されている）
- 1/5 is in simplest terms. （1/5 は既約分数である）
- 1/5 is in lowest (lower) terms. （1/5 は既約分数である）
既約分数を表す表現はいろいろありますが、既約分数にすることは「reduce to its lowest terms」という形でほぼ慣用句として使われています。
ここでの「its」は、約分する分数を指します。
- The fraction is already in its lowest terms. （分数は既約分数である）
- Reduce 6/36 to its lowest terms. （6/36 を既約分数にしなさい）
上の表現で何度か「terms」という単語を使いましたが、これは「denominator」と「numerator」の両方を指して言う場合の表現です。「common factor of numerator and denominator」などというのが大変なので「common factor of these terms」とするとシンプルになります。
「term/ terms」は「第１章：加減乗除の英語表現（上級）」で紹介したように、単に「項」を表します。
なので、項が分母・分子を表していると分からない場面で、急に「common factor of these terms」と言っても「何の項？」となってしまうことに注意してください。
通分について
少し確認をすると、通分とは「分母の異なる二つ以上の分数を、それらの値を変えないで分母の等しい分数にすること」でした。
まず、通分することは、「reducing the fractions to a common denominator」と呼びます。
ここでいう「common denominator」とは、「共通分母」のことです。
また、「common denominator」の中で最小のものを「the least common denominator」もしくは「the lowest common denominator」と言います。
例えば、1/6 と 1/4 を通分したいとき、これらの共通分母は１２の倍数です。
その中で最小の共通分母は、１２となります。
「第１章：倍数・約数・余りの英語表現（初級）」で習った、「least common multiple（最小公倍数）」との関連を見てみると、「least common denominator」とは、通分する分数の分母の「least common multiple」だということがわかると思います。
さらに、分母の異なる分数のことを「unlike fractions」と言います。
「unlike」には「同じでない、異なった」という意味があります。
もちろん、「fractions with different numerators」と言ってもかまいません。
- Find a common denominator of 1/7 and 3/16. （1/7 と 3/16 の共通分母を求めなさい）
- Reduce 1/2 and 1/3 to the lowest common denominator. （1/2 と 1/3 を通分しなさい）
- Add 1/2 and 1/3 by reducing the fractions to a common denominator. （通分することで 1/2 と 1/3 を足し合わせなさい）
- Convert the pair of unlike fractions to that of like fractions. （分母の異なる分数の組を共通分母の組に変化しなさい）
＊convert：変える、変換する
ここまでで、約分と通分の両方に「reduce（減らす）」という単語を使いました。
約分の方は、分母と分子の数を約数で割ることで小さくするので、「減らす」動作がわかります。
では、通分の方はどこで減らしているのでしょうか？
例えば、「1/63 と 1/36 を通分しなさい」と言われたら、直接最小の共通分母を探すこともできます。
しかし、一度二つの分数の和を求め、その後約分するのが最も古典的です。
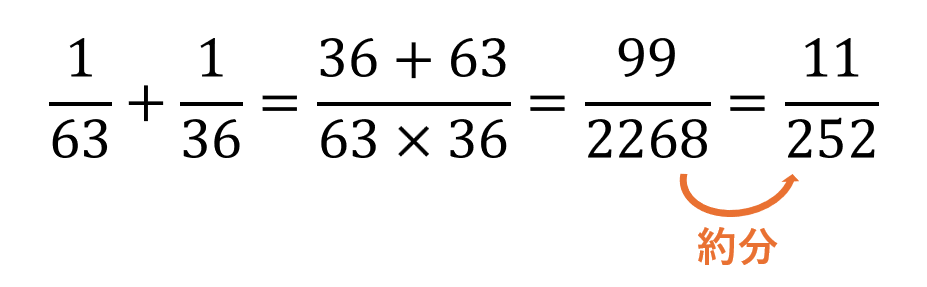
この最後の約分が「reduce」を指しています。
逆数について
逆数とは「ある０でない数が与えられたときに、その数との積が１になる数」のことでした。
たとえば、２の逆数は 1/2 で、2/3 の逆数は 3/2 となります。
逆数は英語で「reciprocal」もしくは「(multiplicative) inverse」と言います。
中学・高校では「reciprocal」が一般的です。
しかし大学に入ると、逆数を含めたより広い意味で「multiplicative inverse」という単語をよく使うようになります。
なので、正確には「reciprocal = multiplicative inverse」ではありません。
ただ単に「逆数」と言いたい場合は「reciprocal」を使う方がいいでしょう。
- The reciprocal of 3 is one-third. （３の逆数は、1/3 である）
- The product of a fraction and its reciprocal is 1. （ある分数とその逆数の積は１になる）
３などの整数の逆数を考えるときに、分母に見えない１があると考えると分かりやすいと教わったことがあるかもしれません。英語圏では、この分母の１を「invisible denominator」と言われることがあります。「invisible」はそのまま「目に見えない」という意味です。
例：The number 3 is a whole number, so it has an invisible denominator of 1.
練習問題
Which one of the following statements is true?
- 3/21 is irreducible.
- The least common denominator of 1/3 and 1/5 is 12.
- When a fraction is multiplied by its reciprocal, the result is always one.
解答
問題の和訳：次のうちどの文章が正しいですか？
- 3/21 は既約分数である
- 1/3 と 1/5 の共通分母は12である
- ある分数にその逆数をかけたとき、その結果はいつも１になる
正解：C
A fraction where the numerator is smaller than the denominator is called a “proper fraction（真分数）”. On the other hand, the one with the numerator greater than the denominator is called an “improper fraction（仮分数）”.
Is the following statement true based on the above definitions?
- The reciprocal of a proper fraction is always an improper fraction.
If not, point out the mistake in the statement.
解答
No. The reciprocal of a proper fraction is an improper fraction ”or an integer”.
問題の和訳：
分子が分母よりも小さい分数を”真分数”と言います。逆に、分子が分母よりも大きいものを”仮分数”と言います。
上の定義をもとにすると、次の文章は正しいと言えますか？
- 真分数の逆数は仮分数である
もし違うのなら、この文章の間違いを指摘しなさい。
＊例えば、1/3 の逆数は３で整数であり分数ではありません
2つ目の問題は問題文が長かったので、難しく感じた人も多かったかもしれません。和訳なども見ながら確認してください。
真分数・仮分数については、次の上級の記事で扱います。
単語のまとめ
| 単語・表現 | 意味 |
|---|---|
| reducing fractions | 約分 |
| simplifying fractions | 約分 |
| reduce A to B | A を B に約分する |
| simplify A to B | A を B に約分する |
| reduce to its lowest terms | 既約分数にする |
| （分数に対して言うときの）terms | 分母と分子の両方を指す単語 |
| reducing the fractions to a common denominator | 通分 |
| common denominator | 共通分母 |
| the least common denominator | 最小の共通分母 |
| the lowest common denominator | 最小の共通分母 |
| unlike fractions (もしくは fractions with different denominators) | 分母の異なる２つ以上の分数 |
| reciprocal | 逆数 |
| (multiplicative) inverse | 逆数 |
最後に
いかがだったでしょうか？
今回の内容はかなり簡潔で特に初級から難しくなったわけではないと思います。ですが、細部まで読んで見落としがないか確認するとより深い理解が得られると思います。
次の上級では、さらに細かく分数の英語表現を見ていきます。
コメント