第11章：平面図形の特徴と種類（中級）

Table of Contents

はじめに
単語の解説
最後に

はじめに

今回は、初級に引き続き「平面図形の特徴と種類」を見ていきます。この記事では、特に三角形・四角形・円などの図形の名称を詳しく見ていきます。

語源などについても解説していますので、より詳しく単語の意味を知りたい方は参考にしてください。

また、今回の記事は初級の記事の知識を必要とします。まだ初級の記事を読んでいない方や、多角形やより細かい話題について解説した上級の記事を読みたい方は、以下のリンクから飛んでください。

→ 平面図形の特徴と種類（初級）
→ 平面図形の特徴と種類（上級）

（所要時間：１０分）

単語の解説

三角形の種類

三角形は英語で「triangle」と言います。
三角形の種類で習うものは主に次の５つです：

種類	説明
直角三角形	一つの角が直角である三角形
二等辺三角形	二つの辺の長さが等しい三角形
正三角形	すべての辺の長さが等しい三角形
鋭角三角形	三つの内角がすべて90°よりも小さいような三角形
鈍角三角形	一つの内角が90°よりも大きいような三角形

英語では次のように言います。

種類	英語
直角三角形	right triangle もしくは right-angled triangle
二等辺三角形	isosceles triangle
正三角形	equilateral triangle もしくは regular triangle
鋭角三角形	acute triangle もしくは acute-angled triangle
鈍角三角形	obtuse triangle もしくは obtuse-angled triangle

正三角形を「regular triangle」とも言いますが、これについては次の（上級）記事の「多角形」で解説しています。

語源の紹介

「isosceles」

この単語はギリシャ語の「isos（等しい）」と「skelos（脚）」を組み合わせたのが語源です。
そのため、「isosceles」は「等脚である」という意味になります。
下で紹介しますが、二等辺三角形の等しい２辺を英語では「leg（脚）」と呼びます。

「equilateral」

この単語は「equi（等しい）」と「lateral（側部、側面）」から構成されています。
このことから、「equilateral triangle」は「すべての辺の長さが等しい三角形」すなわち「正三角形」となります。

また、二つのタイプが使われた「直角二等辺三角形」は「isosceles right triangle」と呼びます。
そのままですね。

三角形に関連する単語

ここからは、小学校で習った三角形に関連する単語を紹介します。

直角三角形

直角三角形の辺は二つの種類に分けられます。

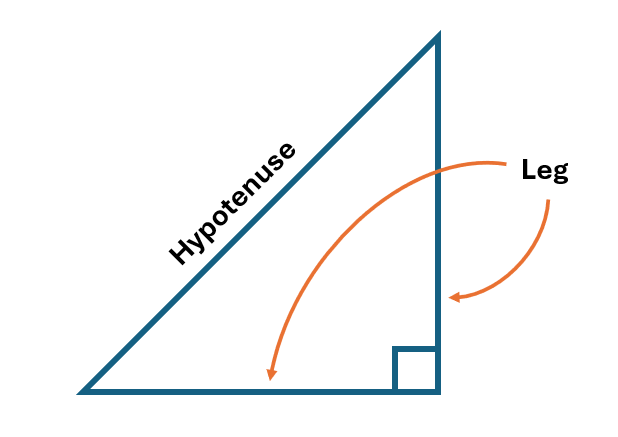
「斜辺」：「直角の対辺」
「隣辺りんぺん」：「直角ととなり合う２辺」

ここで、「斜辺」は「hypotenuse」、「隣辺」は「leg」または「cathetus」と言います。

「cathetus」の複数形は「catheti」です。

二等辺三角形

二等辺三角形にはそれぞれの辺と角、点に名前があります。

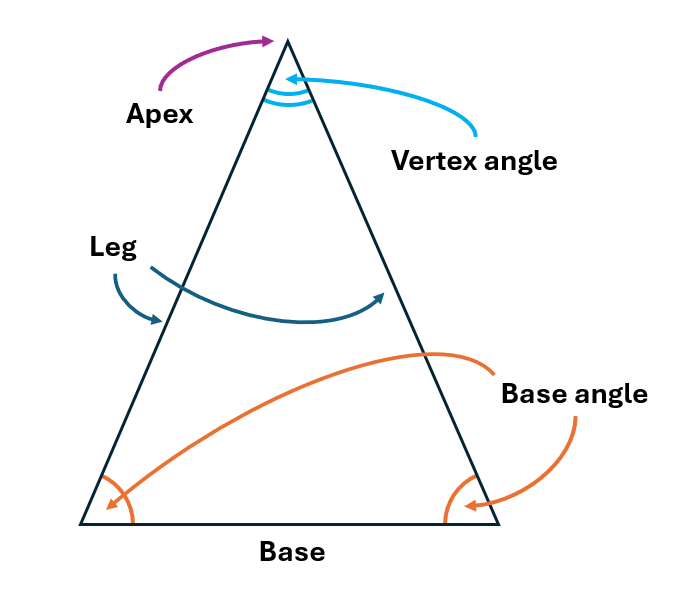
「等辺」：「長さの等しい２辺」
「底辺」：「他の２辺と長さの等しくない辺」
「頂角」：「２つの等辺の間の角」
「底角」：「頂角以外の残りの２つの内角」
「（二等辺三角形の）頂点」：「底辺の対頂点」

ここで、これらの名称は英語で次のように表されます。

名称	英語
等辺	leg
底辺	base
頂角	vertex angle
底角	base angle
（二等辺三角形の）頂点	apex

直角三角形と二等辺三角形の両方で「leg」という単語が使われていますが、どちらも基準の角から見た「脚」を表しているためこの単語が使われています。
この後に出てくる台形の「leg」も同じ解釈ができます。

「vertex」と「apex」の意味と違い

普通に「頂点」というときは、単に「それぞれの角の端にある点」という認識です。
しかし、二等辺三角形の「頂点」は、「底辺の対頂点」を表します。

英語ではこれらの２つの単語の認識は少し異なり、次のようになります。

「vertex」

「vertex」は「複数の線の交点」という意味です。
このことから、一般に図形の「頂点」を表します。

「apex」

「apex」には「最も高い位置にある」といった意味合いがあります。
よって「底辺」を底と考えたとき、その上にある頂点は最も高い位置にあり「apex」となります。

「vertex」の複数形は「vertices」もしくは「vertexes」、「apex」の複数形は「apices」です。

四角形の種類

まず、四角形は英語で「quadrilateral」や「tetragon」、「quadrangle」などと言います。

「quadrangle」の「quad」はラテン語の「４」を表し、「angle」はそのまま「角」を指します。
そこから、「４つの角」という意味だと分かると思います。

それに対して、「equilateral」の語源でも説明したように「quadrilateral」の「lateral」は「辺」を表します。
ここから、「quadrilateral」は「４つの辺」すなわち「四辺形」であると言えます。

さらに、「tetragon」はギリシャ語の「tetra（４）」と「gon（角）」を組み合わせた単語です。

一般的には上の３つの単語が使われる頻度は少なく、下のような四角形の種類で表現する場合が多いです。

種類	説明
長方形	すべての角が直角な四角形
正方形	すべての角が直角ですべての辺の長さが等しい四角形
ひし形	すべての辺の長さが等しい四角形
台形	少なくとも一組の向かい合う辺が平行である四角形
平行四辺形	向かい合う二組の辺がそれぞれ平行である四角形

英語では次のように言います。

種類	英語
長方形	rectangle
正方形	square
ひし形	rhombus もしくは equilateral quadrilateral
台形	trapezoid (アメリカ英語) もしくは trapezium (イギリス英語)
平行四辺形	parallelogram

正方形を「regular tetragon」とも言いますが、これについても次の（上級）記事の「多角形」で解説しています。

語源の紹介

「rectangle」

ラテン語の「rectus（直角）」と古フランス語の「angle（角）」を組み合わせて出来た単語です。

「rhombus」

ギリシャ語の「rhómbos（回転するもの、円運動）」という単語が語源です。
なぜそれがひし形になったのかという歴史的背景は分かりませんでした。

「trapezium」

ギリシャ語の「trapezion（小さなテーブル）」が語源です。

「trapezoid」

ギリシャ語の「trapezoeidé」が語源です。
「trapeza（テーブル）」と「-oeides（形の）」から構成され、「テーブル型の」という意味です。
古代ギリシャの数学者ユークリッドによって「台形型の図形」という意味になりました。

「parallelogram」

ギリシャ語の「parallēló-grammon（平行な線に囲まれた）」が語源です。

四角形に関連する単語

台形

台形についての名称には次のようなものがあります。

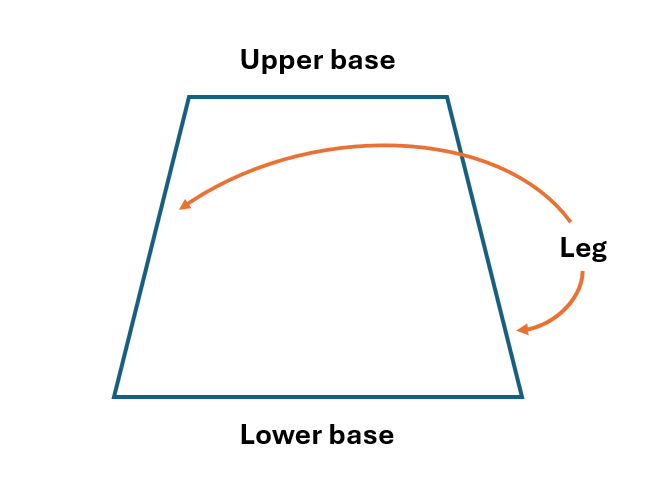
「（台形の）底辺」：「平行な２本の対辺」
「上底」：「底辺のうちで上にある辺」
「下底」：「底辺のうちで下にある辺」
「台形の脚きゃく」：「底辺でないもう１組の対辺」

「台形の脚」は平行でない必要があります。
並行である場合には、台形は平行四辺形となり、２組とも「底辺」となります。

これらを英語では次のように言います。

名称	英語
（台形の）底辺	base
上底	upper base もしくは top base
下底	lower base もしくは bottom base
台形の脚	leg もしくは lateral side

円

まず、円は英語で「circle」と言います。
また、円に関連する単語には次のようなものがあります。

用語	英語
円周	circuference
円周率	π もしくは pi
直径	diameter
半径	radius
（円の）中心	center
（円の）弦げん	chord
（円の）弧こ	arc
扇形おうぎがた	(circular) sector
弓型	(circular) segment
半円	semicircle

「radius」の複数形は「radii」になります。

これらは次の図の部分を表します。

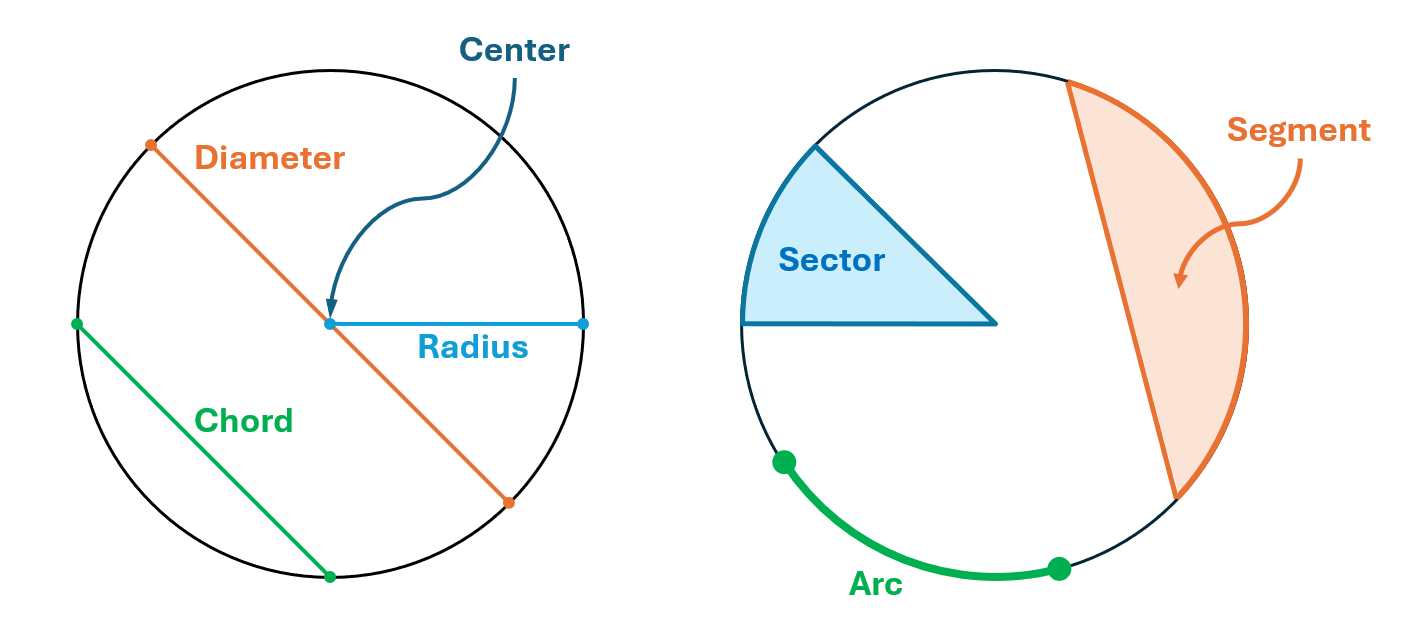
また、楕円だえんは英語で「ellipse」と言います。

楕円を「oval」を使う場合もあるようですが、数学の中では「楕円 = oval」ではありません。

最後に

いかがでしたか？

今回の内容は、初級に比べて情報量も多く記憶しないといけない単語も多いので、覚えるのには時間がかかるかもしれません。まずは、それぞれの図形の種類を英語で言えるようにし、その後細かい名称を覚えるのがいいでしょう。

次の上級では、多角形やより細かい話題について扱います。最後まで読んでいただきありがとうございました。