はじめに
今回は、初級・中級に引き続き「分数の英語表現」を解説していきます。上級の記事では「分数の種類」と「難しい分数の表現や使い分け」に解説していきます。初級・中級に比べて難易度が上がり、また、重要度は下がるので、全体を理解してもらえれば十分です。
この記事は、基本的な内容を扱った初級と中級の記事のプラスアルファとしての内容です。まだ、初級と中級を読んでいない方はそちらを先に読むことをおすすめします。
→ 分数の英語表現(初級)
→ 分数の英語表現(中級)
この記事には練習問題はありません。
(所要時間:10~15分)
単語・表現の一覧
| 単語・表現 | 意味 |
|---|---|
| proper fractions | 真分数 |
| improper fractions | 仮分数 |
| positive proper (improper) fractions | 〈分母と分子が正の数のときの〉真分数(仮分数) |
| mixed fractions | 帯分数 |
| decimal fractions | 小数 |
| compound fractions | 繁分数 |
| complex fractions | 繫分数 |
| define | 定義する |
単語の解説
分数の種類①(真分数・仮分数)
まず、真分数・仮分数の意味を確認します。
真分数:分子が分母よりも小さい分数(* 1/2 や 2/5 など)
仮分数:分子が分母よりも大きい分数(* 3/2 や 7/3 など)
これを英語では、真分数を「proper fraction」、仮分数を「improper fraction」と言います。
分子と分母の両方が正の数のときに、「positive proper fraction」と「positive improper fraction」ということがあります。
真分数・仮分数という単語自体は覚える必要はないですが、「proper/ improper」という単語は数学で覚えておいてもいいと思います。
例えば、高校数学では「proper/ improper sets」というものを習います。「ある条件を満たしているかどうか」という意味で、「proper」と「improper」に分けることは数学でよくあります。
分数の種類②(帯分数)
帯分数とは、仮分数を「整数部分と真分数」の形で表す分数のことです。
英語では「mixed fraction」と言います。
例えば、ハリーポッターに出てくる「9と4分の3番線」を例にしてみると次のような関係になります。

帯分数の読み方は「nine and three-quarters」というように、「(整数部分)and(初級での分数の読み方)」となります。
「nine and three over four」としても同じ意味になります。
帯分数を「mixed number(混数)」とすることもありますが、これは正確には「mixed fraction(帯分数)」と「mixed decimal(帯小数)」の両方を指しています。
分数の種類③(小数)
小数は、10や100を分母にもつ分数と考えると分数の一つと言うこともできます。
そのため小数は、そのような形で表されるとき、英語で「decimal fraciton」と呼ばれます。
詳しい説明は、次の記事で紹介したいと思います。
分数の種類④(繁分数)
繁分数とは「分数の分母または分子の中に分数を含むもの」を言います。
これは「compound fraction」もしくは「complex fraction」と言います。
例えば、次のような繫分数は以下のように読めます。
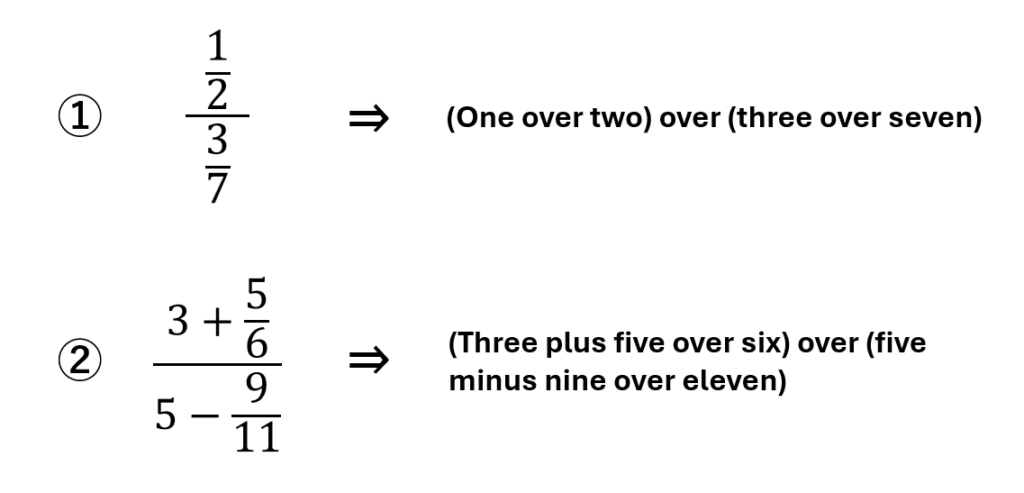
*分かりやすさのために、分母と分子を()でくくっていますが、実際には必要ないです。
ここで注意点を紹介します:
- 当たり前ですが、上のような繫分数を口頭で言っても相手は理解できません。
上のような言い方は、相手が目で追える状況でのみ使いましょう。 - 上では「over」のみを使いましたが、「one over two divided by three over seven」というようにすると、分母と分子の分かれ目がはっきりします。
- 初級で紹介した「one-third」のような表現は避けた方がいいでしょう。
自分でも言いづらい上に、相手にも通じにくくなります。
その他の分数の種類
その他の分数の種類を軽く紹介します。
Like fractions and unlike fractions
中級でも紹介しましたが、分母の等しい分数を「like fractions」、分母の異なる分数を「unlike fractions」と言います。
Equivalent fractions
例として、1/2 と 2/4 はどちらも同じ分数を表しています。
このように違う形でも同じ値の分数を「equivalent fractions」と言います。
Ratio
小学6年生で習う「比、比率」は、英語で「ratio」と言います。
1/2 を 1:2 と表すことができるので、比も分数の表現方法だと言えます。
Percentage
私たちも日常で使う「90%」という表記も、90/100 と表すことができるので、分数の一種です。
英語ではこれを「percentage」といい、実際に「90%」などと言うときは「ninety percent」と言います。
Unit fraction
分子が1である分数のことを「unit fraction」と言います。
「unit」は「一単位当たりの」というような意味になります。
3/5 などを「1/5 が3つある」と考えると「1/5」が一単位であることがわかると思います。
Dyadic fraction
分母が2の累乗であるような分数を「dyadic fraction」と言います。
例は、「1/2」、「5/4」や「3/8」などです。
二進数を使うコンピューターサイエンスなどで使われる分数です。
分数として表せない形
一般に、「0で割る」という行為は数学では「定義」されません。
「定義する」を「define」というので、「0での割り算は定義できない」は「the division by zero is undefined」と言いうことができます。
高校や大学に入ると「定義」という言葉を使うようになります。
「0での割り算」は一般的ですが非常に面白い話題なので、興味のある方は調べてみると数学により興味を持てるかもしれません。
分数の表現方法①でのhyphenの使い方
初級で述べたように、「one-third」などの「hyphen」を使う表現には、文法による厳密なルールがあります。
私は文法の専門家ではないので、ここでは数学に関わる部分での使い分けのみを紹介します。
まず分数は、「名詞」と「名詞の前の形容詞」、「名詞の前の数量詞」の三つの場面で使われます。
名詞の場合
分数を名詞として使う場合には、例えば「two-thirds」と「two thirds」では意味合いが変わってきます。
hyphenを使う場合は、そのまま「2/3」という分数を表すのに対して、hyphenがない場合は、「2つの 1/3 がある」と解釈されます。
普通は hyphen を使いますが、「1/3 が2つある」と強調したいときのみ hyphen を外すと考えるといいと思います。
名詞の前の形容詞の場合
例えば、「2.5時間の勉強」を英語で言うと「two-and-a-half-hour studies」となります。
この青いハイライトの部分は、名詞「studies」の前の形容詞なので、「hour」も含めてhyphen を使います。
名詞の前の数量詞の場合
例えば、「私は2.5時間勉強した」を英語で言うと「I studied two and a half hours」となります。
このときの「2.5」は時間としての数量を表しているので、hyphen は使いません。
wholeの使い方
分数を使う場面では、分数と整数の違いを明確にするために、整数に「whole」をつける場合があります。
例えば、3のことを強調して「three wholes」という場合があります。
「whole」は、ヨーロッパでの分数の考え方とも非常に関係があります。
より詳しい解説は下の記事で紹介しています:
→ 関連記事は現在作成中です。

解説は以上です。お疲れさまでした。
単語のまとめ
| 単語・表現 | 意味 |
|---|---|
| proper fractions | 真分数 |
| improper fractions | 仮分数 |
| positive proper (improper) fractions | 〈分母と分子が正の数のときの〉真分数(仮分数) |
| mixed fractions | 帯分数 |
| decimal fractions | 小数 |
| compound fractions | 繁分数 |
| complex fractions | 繫分数 |
| define | 定義する |
最後に
最後まで読んでいただきありがとうございました。
かなり細かくまとめたので全体の量が多くなってしまいました。自分の中で重要だと思う部分を中心に読むだけでも十分ためになると思います。
次の章では「小数」について扱います。次の記事もぜひ読んでください。




コメント